Exercício 02

                                    Atividade das páginas: 115,116,135 e 136

1. Escreva a Função afim F(X) = ax+b , Sabendo que :

A-    f(1)= 5 e f(-3)= -7

B-    f(-1)=7 e f(2)= 1

Resposta

A-    f(x) = ax + b

f(1) = 5f(-2) = 35 = a*1 + b3 = a*(-2) + b{a + b = 5{-2a + b =b = 5 - a-2a + 5 - a = 3-3a = -2a = 2/3b = 5 - 2/3b = 13/3f(x) = 2x/3 + 13/3

B-    -a + b =7(2)

2a +b = 1

-2a +2 b =14

  2a +b = 1

        3a=15

          a=3

-3 + b = 7

       b=7+3 = 10

Y = 3a + 10

    

B- f(1)=5 e f(-2)=4

a + b = 5(2)

-2a + b = 4

2a + 2b =10

-2a + b = 4

        3b= 14

            b=14/3

a + b = 5

a = 5 - 14/3

a = 15-14

           3

a=   1

        3

Y = 1/3 x + 14/3

2. A função que representa o valor a ser pago após um desconto de 3% sobre o valor x de uma mercadoria é?

Resposta

x-3%de x=

=x-0,03x

f(x)=0,97x 

3. Uma cidade é servida por duas empresas de telefonia. A empresa X cobra, por mês, uma assinatura de R$ 35,00 mais R$0,50 por minuto utilizado. A empresa Y cobra, por mês, uma assinatura de R$26,00 , mais R$0,65 , por minuto utilizado . A partir de quantos minutos de utilização o plano da empresa X passa a ser mais vantajoso p/ os clientes do que o plano da empresa y ? 

Resposta

f(x)=35+0,5x

O preço da segunda obedece a outra função

f(x)=26+0,65

35+0,5x=26+0,65x

0,15x=9

15x/100=9

15x=900

x=60

4.Um comerciante teve uma despesa de R$230,00 na compra de certa mercadoria como, vai vender cada unidade por R$ 5,00 o lucro final será dado em função das x unidades vendidas.

A)  qual a lei dessa função

F?

B) Para que valores de x temos f(x)<0? como pode ser interpretado esse caso?

C) Para que valor de x haverá um lucro de 315,00

D) Para que valor de x o lucro será maior que R$ 280,00?

E) Para que valor de x o lucro estará entre R$ 100,00 e R$180,00

Resposta

A)  F=5*x-230 OBS:5*x=5vezes x

B) 5*x-230<0

x<230/5

x<46

C) 5*x-230=315

5*x=545

x=109

D) 5*x-230>280

5*x>510

x>510/5

x>102

E) 100<5*x-230<180

somando-se 230 em todos os pontos da equação temos:

100+230<5*x-230+230<180+230

330<5*x<410

Agora dividindo tudo por cinco:

330/5<5*x/5<410/5

66<x<82

5. Verifique quais das funções abaixo sãos afins usando f(x + h) - f(x). 

f(x) = -6 + 1                                    g(x) = x² - 5x

Resposta

Acho que é f(x) = -6x + 1. Então,

f(x+h)-f(x) = (-6(x+h) + 1)- (-6x+1) = -6x -6h +1 +6x -1 = -6h (que não depende de x: é afim).

g(x) = x^2 - 5x

g(x+h)-g(x) = (x+h)^2 – 5(x+h) – (x^2-5x) = x^2 +2xh +h^2 -5x -5h – x^2 + 5x = 2xh-5h+h^2 (que depende de x e por tanto g(x) não é afim).

6. Determina a lei da função afim , sabendo que f(2) 11 e f(-3) = -4  .

 

F(x) =ax+b

F(2) = 2.a.b=11

F(-3) =ax+b

F(-3)=-3.a+b=-4

{2.a+b=11

{-3.a+b=-4 .(-1)

2.a+b=11

3.a-b=4

5a=15

  a=15/5

    a=3

 

 

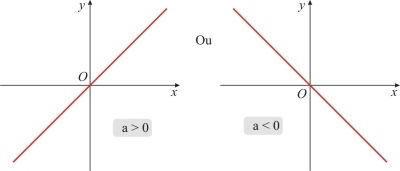
7. determine o valor de k e R de modo que a função F(x) (3k – 18 ) x+7 seja decrescente .

 

                                  Solução .

A <0

3k-18<0

3k<18

K < 18/3

K <6 

 

8.Resolva o sistema de inequação em IR

 

        A - x+1> -2x-4

       x + 1 > -2x - 4

        x + 2x > -4 - 1

         3x > -5

           x > -5/3

        S: {x ϵ IR / x > -5/3}

Por: Todos componentes. 

Função linear

Uma função definida por f: R→R chama-se linear quando existe uma constante a ∈ R tal que f(x) = ax para todo x ∈ R. A lei que define uma função linear é a seguinte:

O gráfico da função linear é uma reta, não perpendicular ao eixo Ox e que cruza a origem do plano cartesiano.

Domínio: D = R
Imagem: Im = R

        

 

 Exemplos 



Esboce o gráfico:
a) f(x) = 2x + 3
b) f(x) = 3x – 2
c) y = –x + 1
d) f(x) = –2x + 2
e) y = –x – 2
f) f(x) = x + 3 

     - Gráficos .      


a)

b) 


c) 
 
d) 

e)
 
f)
 

 

 

 Função constante

Uma função definida por f: R→R chama-se constante quando existe uma constante b R tal que f(x) = b para todo x ∈ R. A lei que define uma função constante é:

O gráfico de uma função constante, é uma reta paralela ou coincidente ao eixo Ox q que cruza o eixo Oy no ponto de ordenada b.

Função Crescente e Decrescente

As funções que são expressas pela lei de formação y = ax + b ou f(x) = ax + b, onde a e b pertencem ao conjunto dos números reais, com a ≠ 0, são consideradas funções do 1º grau. Esse tipo de função pode ser classificada de acordo com o valor do coeficiente a, se a > 0, a função é crescente, caso a < 0, a função se torna decrescente.

Vamos analisar as seguintes funções f(x) = 3x e f(x) = –3x, com domínio no conjunto dos números reais, na medida em que os valores de x aumentam.



Exemplo 1
f(x) = 3x

Note que à medida que os valores de x aumentam, os valores de y ou f(x) também aumentam, nesse caso dizemos que a função é crescente e a taxa de variação da função é igual a 3.

Exemplo 2 f(x) = –3x

Nessa situação, à medida que os valores de x aumentam, os valores de y ou f(x) diminuem, então a função passa a ser decrescente e a taxa de variação tem valor igual a –3.

Outro fato importante para designar uma função é o seu gráfico, note que quando a função é crescente o ângulo formado entre a reta da função e o eixo x (horizontal) é agudo (< 90º) e na função decrescente o ângulo formado é obtuso (> 90º).

Então, a função é crescente no conjunto dos números reais (R), quando os valores de x1 e x2, sendo x1 < x2 resultar em f(x1) < f(x2). No caso da função decrescente no conjunto dos reais, teremos x1 < x2 resultando em f(x1) > f(x2).

Por: Todos componentes.