Matemática Amiga
segunda-feira, 13 de janeiro de 2014
sábado, 21 de dezembro de 2013
Função quadrática
Em matemática, uma função quadrática é uma função polinomial da forma:
 é 2.
é 2.Se a função quadrática é igualada a zero, o resultado é uma equação quadrática. As soluções para a equação são chamadas raízes da equação ou os zeros da função, e são os interceptos do gráfico da função com o eixo x.
- Raizes
As raízes da função quadrática são os valores de x cuja imagem é 0, ou seja, em que o gráfico corta o "eixo x". O número de raízes depende do valor do discriminante, geralmente denotado pela letra grega delta, definido por:
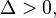 a função terá duas raízes.
a função terá duas raízes.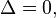 a equação terá uma raiz apenas (com maior precisão, diz-se que a equação tem duas raízes iguais)
a equação terá uma raiz apenas (com maior precisão, diz-se que a equação tem duas raízes iguais)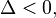 não terá raíz (com maior precisão, diz-se que a equação não tem raíz reais, tendo duas raízes complexos conjugados).
não terá raíz (com maior precisão, diz-se que a equação não tem raíz reais, tendo duas raízes complexos conjugados).
 onde
onde  são
são
Essa fórmula é chamada de Fórmula de Bhaskara.
- Dado

- Se
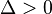 , então existem duas raízes distintas uma vez que
, então existem duas raízes distintas uma vez que  é um número real positivo.
é um número real positivo. - Se
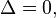 então as duas raízes são iguais, uma vez que
então as duas raízes são iguais, uma vez que  é igual a zero.
é igual a zero. - Se
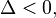 então as duas raízes são números complexos conjugados, uma vez que
então as duas raízes são números complexos conjugados, uma vez que  é imaginário.
é imaginário.
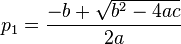 e
e 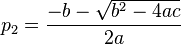 ou vice versa, é possível fatorar
ou vice versa, é possível fatorar 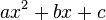 como
como 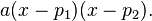
Concavidade do gráfico da função quadrática
A concavidade é a abertura da parábola, que ora está voltada para cima e ora está voltada para baixo. O sentido da concavidade depende do coeficiente a, se este for superior a 0, ou seja, positivo, ela é voltada para cima, caso seja negativo ela é voltada para baixo.Vértice da parábola
O vértice da parábola corresponde ao ponto mais extremo dela. É definido pelas seguintes coordenadas:Crescimento e decrescimento de uma função quadrática
Em uma parábola, metade é crescente e a outra metade é decrescente.- Concavidade voltada para cima:
- Decrescente do -infinito ao vértice
- Crescente do vértice ao infinito
- Concavidade voltada para baixo:
- Crescente do -infinito ao vértice
- Decrescente do vértice ao infinito
Formas da função quadrática
Uma função quadrática pode ser expressa em três formatos: é chamada a forma geral ou forma polinomial (também chamada de forma desenvolvida),
é chamada a forma geral ou forma polinomial (também chamada de forma desenvolvida),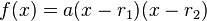 é chamada a forma fatorada, onde
é chamada a forma fatorada, onde 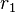 e
e 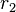 são as raízes da equação quadrática, e
são as raízes da equação quadrática, e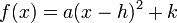 é chamada a forma padrão ou forma vértice (também chamada de forma canônica).
é chamada a forma padrão ou forma vértice (também chamada de forma canônica).
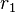 e
e 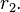 Para converter a forma geral para a forma padrão é necessário usar o processo de completar o quadrado. Para converter a forma fatorada (ou padrão) para a forma geral, é necessário multiplicar, expandir e/ou distribuir os fatores.
Para converter a forma geral para a forma padrão é necessário usar o processo de completar o quadrado. Para converter a forma fatorada (ou padrão) para a forma geral, é necessário multiplicar, expandir e/ou distribuir os fatores.Gráfico
Independentemente do formato, o gráfico de uma função quadrática é uma parábola (como mostrado abaixo).- Se
 a parábola abre para cima.
a parábola abre para cima. - Se
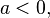 a parábola abre para baixo.
a parábola abre para baixo.
O coeficiente b e a, juntos, controlam o eixo de simetria da parábola (e também a coordenada do x do vértice).
O coeficiente b sozinho é a declividade da parábola ao cortar o eixo y.
O coeficiente c controla a altura da parábola, mais especificamente, é o ponto onde a parábola corta o eixo y.
Vértice
O vértice de uma parábola é o número crítico da função quadrática - o ponto onde ela vira, também chamado de turning point. Se a função estiver na forma padrão, o vértice é dado por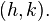 Pelo método de completar o quadrado transforma-se a forma geral:
Pelo método de completar o quadrado transforma-se a forma geral: ou o ponto mínimo se:
ou o ponto mínimo se:- Pontos de máximo/mínimo
- O máximo ou mínimo de uma função é sempre obtido no vértice. O seguinte método se baseia na mesma ideia fazendo uso do cálculo. A vantagem desse método é que ele funciona para funções mais gerais.
- Tomando
 como um exemplo de equação quadrática para achar seus pontos extremos (que dependem de
como um exemplo de equação quadrática para achar seus pontos extremos (que dependem de 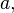 se
se  tem um ponto mínimo, se
tem um ponto mínimo, se 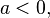 tem um ponto máximo) é necessário antes encontrar sua derivada:
tem um ponto máximo) é necessário antes encontrar sua derivada:
- Depois, encontramos as raízes de
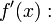
- Então,
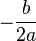 é o
é o  valor de
valor de  Agora, para encontrar o valor de
Agora, para encontrar o valor de  substituimos
substituimos 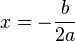 em
em 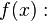
- Assim, as coordenadas do ponto mínimo/máximo são:

Estudo do sinal
O estudo do sinal da função quadrática define o sinal da função para qualquer valor de O estudo depende do sinal do coeficiente
O estudo depende do sinal do coeficiente  e do
e do 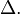 Ele é obtido analisando o esboço do gráfico da concavidade da função.
Ele é obtido analisando o esboço do gráfico da concavidade da função.
Caso Δ < 0
Neste caso, a parábola da função não corta o eixo das absissas. Portanto:
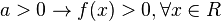
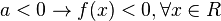
Caso Δ = 0
Neste caso, a parábola da função corta o eixo das absissas em apenas um ponto. Tem-se duas situações, dependendo o valor do coeficiente e das raízes
e das raízes 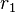 e
e 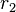 (note que
(note que 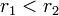 ):
):

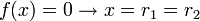
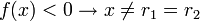
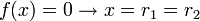
Caso Δ > 0
Neste caso, a parábola da função corta o eixo das absissas em dois pontos. Novamente, tem-se duas situações, dependendo o valor do coeficiente (note novamente que
(note novamente que 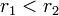 ):
):


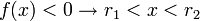
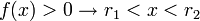

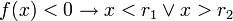
.
Assinar:
Postagens (Atom)








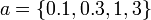


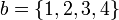

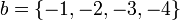
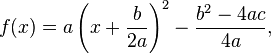
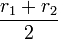

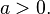


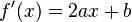
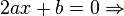
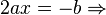
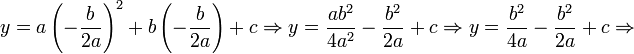
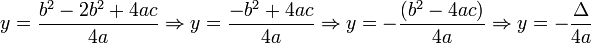


 e nula para
e nula para 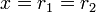


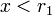 ou
ou 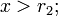 nula para
nula para